数学中考几何(中考几何考什么)

导语：中考几何非常重要的热门基础考点，你会了吗？

提到中考数学，很多人就会想到与几何相关的中考试题，此类题型具有复杂多变、解法灵活、题型丰富、难易可控等鲜明特点，同时又能很好考查考生的几何语言、逻辑推理能力、图形转化能力等，自然成为中考数学热门考点之一。

大家都知道几何的重要性，却很少有人能抓住几何的复习策略，不知道该往哪复习，如一些考生明明是基础知识没有掌握好，却天天拿几何综合问题训练，越练越迷茫，甚至失去学习数学的自信心。

说到几何基础知识内容，我们不得不提平行线。平行线作为初中数学几何内容最重要基础内容之一，很多几何内容都是与平行线息息相关，如相似三角形预备定理。同时，几乎所有中考几何问题都需要用到平行线这个知识内容，才能顺利解决问题。

因此，今天我们就一起讲讲与平行线相关的题型、考点等等，希望能帮助大家提高中考数学几何问题的解题能力。

什么是平行线？

在同一个平面内，不相交的两条直线叫做平行线。平行用符号“∥”表示，如“AB∥CD”，读作“AB平行于CD”。

同一平面内，两条直线的位置关系只有两种：相交或平行。

注意：

1、平行线是无限延伸的，无论怎样延伸也不相交。

2、当遇到线段、射线平行时，指的是线段、射线所在的直线平行。

中考数学，平行线，典型例题分析1：

已知三条不同的直线a、b、c在同一平面内，下列四条命题：

①如果a//b，a⊥b，那么b⊥c； ②如果b//a，c//a，那么b//c；

③如果b⊥a，c⊥a ，那么b⊥c；④如果b⊥a，c⊥a ，那么b//c.

其中真命题的是_________。（填写所有真命题的序号）

解：①如果a∥b，a⊥c，那么b⊥c是真命题，故本选项正确， ②如果b∥a，c∥a，那么b∥c是真命题，故本选项正确，③如果b⊥a，c⊥a，那么b⊥c是假命题，故本选项错误，④如果b⊥a，c⊥a，那么b∥c是真命题，故本选项正确，故答案为①②④．

考点分析：

命题与定理；平行线的判定与性质；推理填空题。

题干分析：

分析是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案。

解题反思：

本题主要考查了命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题，难度适中。

中考数学，平行线，典型例题分析2：

如图，在□ABCD中，AB＝3，AD＝4，∠ABC＝60°，过BC的中点E作EF⊥AB，垂足为点F，与DC的延长线相交于点H，则△DEF的面积是 .

考点分析：

平行四边形的性质；平行线的性质；三角形的面积；三角形内角和定理；含30度角的直角三角形；勾股定理；计算题。

题干分析：

根据平行四边形的性质得到AB=CD=3，AD=BC=4，根据平行线的性质得到∠HCB=∠B=60°，根据三角形的内角和定理求出∠FEB=∠CEH=30°，根据勾股定理求出BF、CH、EF、EH的长，根据三角形的面积公式即可求出答案。

解题反思：

本题主要考查对平行四边形的性质，平行线的性质，勾股定理，含30度角的直角三角形，三角形的面积，三角形的内角和定理等知识点的理解和掌握，能综合运用这些性质进行计算是解此题的关键。

如何判定两条直线是否平行呢？大家一定要记住以下这些重要定理。

平行线平行公理：经过直线外一点，有且只有一条直线与这条直线平行。

平行线平行公理推论：如果两条直线都和第三条直线平行，那么这两条直线也互相平行。

平行线的判定定理1：两条直线被第三条直线所截，如果同位角相等，那么两直线平行。简称：同位角相等，两直线平行。

平行线的判定定理2：

两条直线被第三条直线所截，如果内错角相等，那么两直线平行。简称：内错角相等，两直线平行。

平行线的判定定理3：

两条直线被第三条直线所截，如果同旁内角互补，那么两直线平行。简称：同旁内角互补，两直线平行。

另外补充平行线的3判定方法：

1、平行于同一条直线的两直线平行；

2、垂直于同一条直线的两直线平行；

3、平行线的定义。

中考数学，平行线，典型例题分析3：

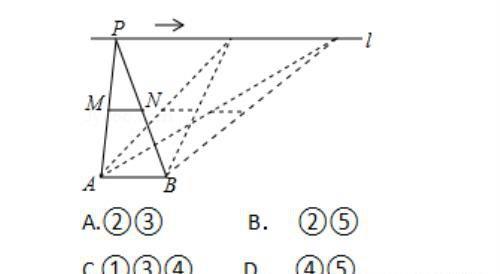
如图，点A，B为定点，定直线l∥AB，P是l上一动点，点M，N分别为PA，PB的中点，对下列各值：

①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小．

其中会随点P的移动而变化的是（　　）

解：∵点A，B为定点，点M，N分别为PA，PB的中点，

∴MN是△PAB的中位线，

∴MN=AB/2，

即线段MN的长度不变，故①错误；

PA、PB的长度随点P的移动而变化，

所以，△PAB的周长会随点P的移动而变化，故②正确；

∵MN的长度不变，点P到MN的距离等于l与AB的距离的一半，

∴△PMN的面积不变，故③错误；

直线MN，AB之间的距离不随点P的移动而变化，故④错误；

∠APB的大小点P的移动而变化，故⑤正确．

综上所述，会随点P的移动而变化的是②⑤．

故选B．

考点分析：

三角形中位线定理；平行线之间的距离．

题干分析：

根据三角形的中位线平行于第三边并且等于第三边的一半可得MN=AB/2，从而判断出①不变；再根据三角形的周长的定义判断出②是变化的；确定出点P到MN的距离不变，然后根据等底等高的三角形的面积相等确定出③不变；根据平行线间的距离相等判断出④不变；根据角的定义判断出⑤变化．

解题反思：

本题考查了三角形的中位线平行于第三边并且等于第三边的一半，等底等高的三角形的面积相等，平行线间的距离的定义，熟记定理是解题的关键．

前面提到平行线的判定定理，需要用到三个角，分别是同位角、内错角、同旁内角。这三种如何去判别，那么大家就需要了解直线相交的相关知识概念。

相交线中的角：

两条直线相交，可以得到四个角，我们把两条直线相交所构成的四个角中，有公共顶点但没有公共边的两个角叫做对顶角。

我们把两条直线相交所构成的四个角中，有公共顶点且有一条公共边的两个角叫做临补角。

临补角互补，对顶角相等。

直线AB，CD与EF相交（或者说两条直线AB，CD被第三条直线EF所截），构成八个角。

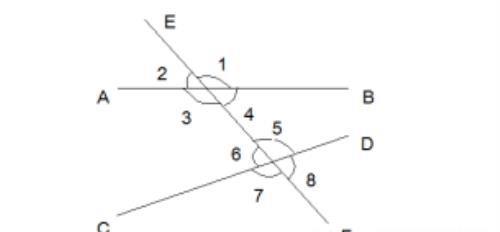
其中∠1与∠5这两个角分别在AB，CD的上方，并且在EF的同侧，像这样位置相同的一对角叫做同位角；

∠3与∠5这两个角都在AB，CD之间，并且在EF的异侧，像这样位置的两个角叫做内错角；

∠3与∠6在直线AB，CD之间，并侧在EF的同侧，像这样位置的两个角叫做同旁内角。

中考数学，平行线，典型例题分析4：

如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是　 　．

考点分析：

平行线的性质；计算题．

题干分析：

过A点作AB∥a，利用平行线的性质得AB∥b，所以∠1=∠2，∠3=∠4=30°，加上∠2+∠3=45°，易得∠1=15°．

解题反思：

本题考查了平行线的性质：两直线平行，内错角相等．

最后记住平行线的性质：

1、两直线平行，同位角相等。

2、两直线平行，内错角相等。

3、两直线平行，同旁内角互补。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小面创作整理编辑！