中考数学图形变换之旋转变换题目(初中数学旋转图形的画法和旋转的性质)

导语：中考数学图形变换之旋转变换

一、旋转变换

指把某个图形按照给定的条件旋转，通过旋转前后图形变换的相互关系来命制的一类问题；

也指解题时需要借助旋转变换构造辅助线帮助问题获得解决的一类问题．

这类题主要考查考生的识图能力、灵活运用知识解决问题的能力等．

二、主要题型

①以旋转为背景的问题；

②利用旋转变换工具解决问题．

三、解题方法

①以旋转为背景的问题

要根据题意，找准对应点，看清对应边，注意旋转性质的理解和运用，想象其中基本元素，

如点、线(角)之间的变化规律，再结合涉及的几何图形性质，大胆地猜想结果并加以验证来解决问题；

②利用旋转变换工具解决问题

要注意观察，通过旋转图形中的部分，运用旋转的性质，将复杂问题简化．

四、例题讲解

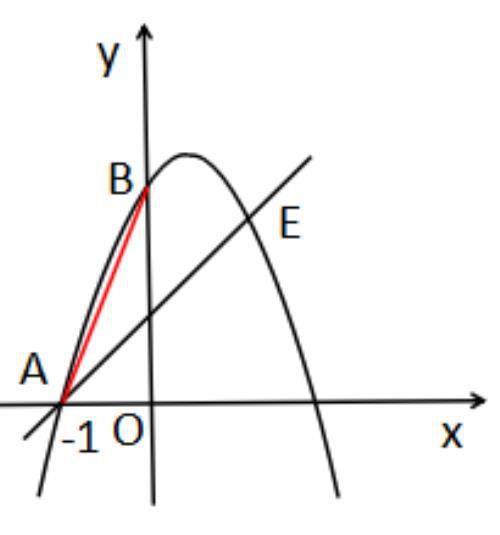
【例题4】如图，抛物线 y＝ax^2＋4x＋c(a≠0) 经过点 A(－1,0)，点 E(4,5)，与 y 轴交于点B，连接 AB.

(1)求该抛物线的解析式；

(2)将 △ABO 绕点 O 旋转，点 B 的对应点为点 F.

①当点 F 落在直线 AE 上时，求点 F 的坐标和 △ABF 的面积；

②当点 F 到直线 AE 的距离为 √2 时，过点 F 作直线 AE 的平行线与抛物线相交，请直接写出交点的坐标．

【解题思路】

(1)根据待定系数法，可得函数解析式；

(2)根据旋转的性质，可得关于 n 的方程，根据自变量与函数值的对应关系，可得 F 点的坐标，根据面积的关系，可得答案；

(3)根据相似三角形的判定与性质，可得 HG＝CG＝√2，

根据勾股定理，可得 HC，

根据平移的规律，可得直线 l，直线 l1，

根据解方程组，可得答案．

【解答过程】

(1)将 A，E 点坐标代入函数解析式，

∴ 抛物线的解析式是 y＝－x^2＋4x＋5，

(2)设 AE 的解析式为 y＝kx＋b，将 A，E 点坐标代入，

∴ AE 的解析式为 y＝x＋1，

当 x＝0 时，y＝1，即 C(0,1)．

设 F 点坐标为(n，n＋1)，

由旋转的性质，得 OF＝OB＝5，

n^2＋(n＋1)^2＝25，解得 n1＝－4，n2＝3，

故 F(－4，－3)，F(3,4)，

当 F(－4，－3) 时，如图(1)，

图（1）

当 F(3,4) 时，如图(2)，

图（2）

(3)如图(3)，

∵ ∠HCG＝∠ACO，∠HGC＝∠COA，

∴ △HGC∽△COA.

∵ OA＝OC＝1，∴CG＝HG＝√2.

由勾股定理，得 HC＝2，

直线 AE 向上平移 2 个单位或向下平移 2 个单位，

L 的解析是为 y＝x＋3，L1 的解析是为 y＝x－1，

∴ F 点的坐标为

【归纳总结】

本题以旋转为背景的综合问题，

解(1)的关键是待定系数法；

解(2)的关键是利用旋转的性质得出关于 n 的方程；

解(3)的关键是利用相似三角形的判定与性质得出 HG＝CG＝√2，

又利用了直线的平移，解方程组求函数图象的交点．

本文内容由小信整理编辑！