亚里士多德认为更重的物体会受到更大的朝向(重物体和轻物体哪个坠落的快)

导语：重物和轻物哪个下落得更快——亚里士多德和伽利略各对了一半

两千多年前的古希腊哲学家亚里士多德认为：物体下落的快慢是由物体本身的重量决定的，物体越重，下落得越快；反之，则下落得越慢。

17世纪时，意大利科学家伽利略对这种观点提出了质疑。他在1638年写的《两种新科学的对话》一书中指出：根据亚里士多德的论断，一块大石头的下落速度要比一块小石头的下落速度大，假定大石头下落速度为8，小石头下落的速度为4，当我们把石头拴在一起时，下落快的会被下落慢的拖着而减慢，下落慢的会被下落快的拖着而加快，结果整体系统的下落速度应该小于8。但是两块石头拴在一起，加起来比大石头还要重，根据亚里士多德的理论，整个系统的下落速度应该大于8。这样就使得亚里士多德的理论陷入了自相矛盾的境地。伽利略由此推断重的物体不会比轻的物体下落得快。

亚里士多德错了吗？未必。

因为亚里士多德并没有说“重的物体和轻的物体从相同的高度同时下落”呀。重的物体和轻的物体下落分两种情况：一、从相同的高度同时下落。二、从相同的高度分别单独下落。（都忽略空气阻力。）

伽利略全对吗？未必。伽利略说对了一半，即“质量不同的两个物体，从相同的高度同时自由落体，忽略空气阻力，这两个物体将同时落地。” 这个观点是对的。

对于质量不同的两个物体，位于相同的高度，忽略空气阻力，它们受到的重力加速度是相同的，所以它们下落时的速度是相同的。对于地球来说，也会以一个微乎其微的速度向它们运动，地球不会偏向任何一个物体。所以这两个物体当然会同时落地。

但伽利略并没有探讨“质量不同的两个物体，从相同的高度，分别单独下落” 的情况。

伽利略并不能证明”质量不同的两个物体，从相同的高度，分别单独下落时，到达地面所用的时间相同。”

事实上，对于质量不同的两个物体，忽略空气阻力，从相同的高度，如果同时下落，它们一定同时着地；如果分别单独下落，则质量大的物体与地球相遇所用的时间短，质量小的物体与地球相遇所用的时间长。

所以亚里士多德也对了一半。

可以简单地设想一下，对于月球，由于万有引力，月球和地球相互吸引，月球向地球靠近，地球同时也会向月球那个方向运动。两者是同时向对方运动的。（理想状态时，两者可以相遇。）

如果此时把月球换成一个10千克的铁球，铁球由于位于原来月球的位置上，它受到的万有引力加速度不变，向地球运动的速度等于之前月球向地球运动的速度。但对于地球来说，受到的万有引力就大大减小了，几乎减小到0，那地球向铁球运动的速度将变得很小，只比0大一点点，接近0。这样铁球与地球相遇就要比月球与地球相遇所用的时间长。

简单地说，月球和地球都是互相拉着对方向自己这边运动，当然两者会更早相遇。月球如果换成铁球，（相同的距离，）相当于只有地球拉着铁球向自己这边运动，铁球对地球的拉力几乎为0，两者相遇时间将加长。

质量不同的两个物体，忽略空气阻力，从相同的高度，分别单独下落，则质量大的物体与地球相遇所用的时间短，质量小的物体与地球相遇所用的时间长。

证明过程如下：

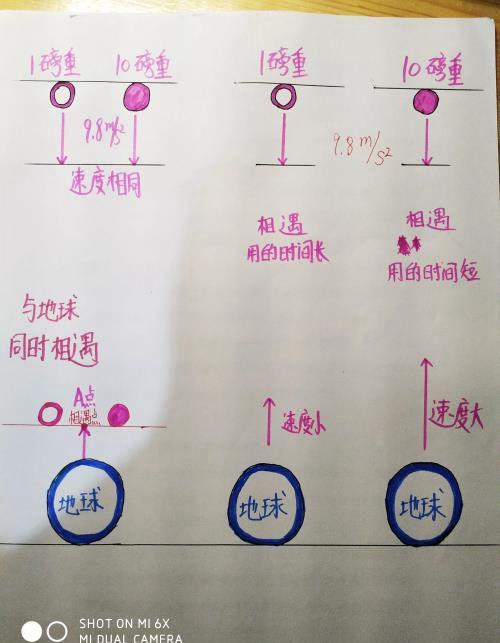
如图

（忽略空气阻力）1磅重的铁球和10磅重的铁球大小相同（可以把1磅重的铁球铸成空心的），它们距离地面的高度相同，都是100米。

万事万物都有万有引力，铁球也有万有引力。

铁球和地球是互相吸引的。铁球落向地球，同时地球也会向铁球运动，不管这个运动的速度有多么慢，距离有多么小，但这个事实是确实存在的。

10磅重的铁球对地球有万有引力，地球便会“奔跑”向它，设“奔跑”的速度是a米/秒。

1磅重的铁球对地球也有万有引力，地球也会“奔跑”向它，设“奔跑”的速度是b米/秒。

质量越大的物体，产生的万有引力越大。所以10磅重的铁球对地球产生的万有引力要大于1磅重的铁球对地球产生的万有引力。

所以a米/秒 大于 b米/秒 。

10磅重的铁球和1磅重的铁球距离地面的高度相同，所以受到的重力加速度是相同的，都是9.8米/秒，所以它们“奔跑”向地球的速度是相同的。

所以地球和10磅重的铁球相遇所用的时间短一些。地球和1磅重的铁球相遇所用的时间长一些。

即10磅重的铁球落地用的时间短，1磅重的铁球落地用的时间长。

总结：对于质量不同的两个物体，忽略空气阻力，从相同的高度，如果同时自由落体，它们一定同时着地；如果分别单独下落，则质量大的物体与地球相遇所用的时间短，质量小的物体与地球相遇所用的时间长。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小森创作整理编辑！