如何做平行线构造相似三角形(平行线型相似三角形)

导语：「初中数学」作平行线构造相似三角形的四种常用技巧

我们在解答相似的习题时，往往会遇到要证的问题与相似三角形联系不上或者说图中根本不存在相似三角形的情况，这时"作平行线构造相似三角形”是解决这类几何证明题的一种重要的方法.常见的情况有:(1)由比例式作平行线;(2)有中点时，作中位线;(3)根据比例式，构造相似三角形.

技巧一.巧连线段的中点构造相似三角形

1.如图，在△ABC中，E，F是边BC的两个三等分点，D是AC的中点，BD分别交AE，AF于点P，Q.求BP:PQ:QD.

【分析】条件，D是AC的中点，E、F是边BC的两个三等分点，所以连接D，F两点，一方面，DF是△AEC的中位线，另一方面，得到△APQ∽△FDQ，所以DF这条辅助线很重要，同时我们看到PE是△BFD的中位线，则DF=2PE，AE=2DF，线段PE，AE在同一条线上，又通过DF联系起来，则AE=4PE，或设PE=K，则DF=2K，则AE=4K，AP=3K，∴AP/DF=PQ/QD=3K:2K=3:2，而PE是△BFD的中位线，∴BP=PQ+QD，∴BP:PQ:QD=5:3:2.如图.

另外，由于E，F为边BC的三等分点，想到平行线分线段成比例，所以过E，F分别作EM∥BD，交DC于M，FN∥BD，交DC于N，则BD∥EM∥FN，如图

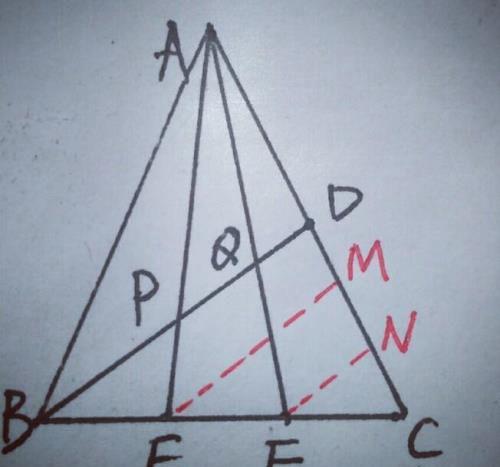
则，DM:MN:NC=1:1:1，由于D为AC的中点，∴QD:FN=AD:AN=3:5，PD:EM=AD:AM=3:4，而FN是△CME的中位线，EM=2FN，设FN=m，EM=2m，则QD=3m/5，则PD=3m/2，PQ=PD一QD=3m/2一3m/5=9m/10，而BD:FN=DC:NC=3，则BD=3m，∴BP=BD一PD=3m一3m/2=3m/2，∴BP:PQ:QD=(3m/2):(9m/10):(3m/5)=5:3:2.

技巧二.过顶点作平行线构造相似三角形

2.如图，在△ABC中，AC=BC，F为底边AB上一点，BF:AF=3:2，取CF的中点D，连接AD并延长交BC于点E，求BE/CE的值

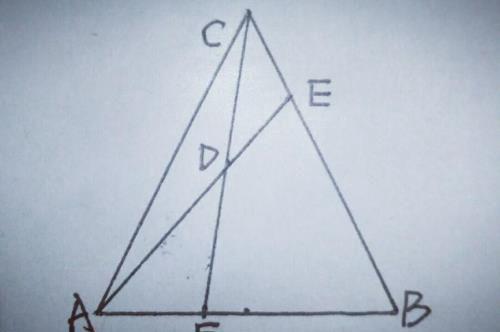
【分析】BF:AF=3:2，与要求的BE/CE连不上关系，那么在不拆BE和CE的条件下，利用平行线进行比的转换，由于D为CF的中点，则过点C作CM∥AB交AE的延长线于M，如图

则可证△ADF≌△MDC，∴AF=CM，由于CM∥AB，∴BE/CE=AB/CM=AB/AF，∵BF:AF=3:2，所以AB:AF=5:2，∴BE/CE=5:2=5/2.

另，过F作FM∥BC，交AD于M，则可证△ADE≌△FDM，∴CE=MF，又BE/MF=AB/AF=5:2，∴BE:CE=5:2=5/2.

另，过B点作BM∥AE，交DF的延长线于M，如图

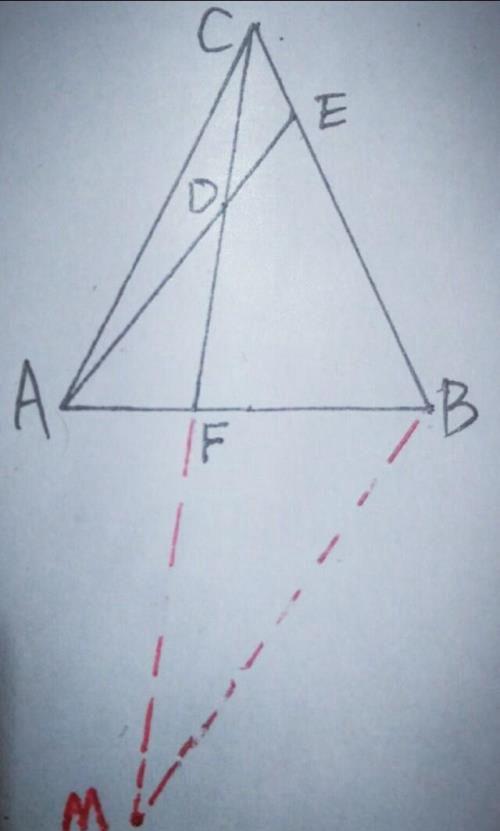
则BE/CE=MD/CD，而MF/DF=FB/AF=3/2，∴MF=3DF/2，设DF=CD=m，则MF=3m/2，∴MD=MF+DF=3m/2+m=5m/2，∴BE/CE=MD/CD=5m/2:m=5/2.

另，过A作AM∥BC，交DF的延长线于M，如图

则AM/CB=MD/CD，AM/CB=AF/FB=2/3=MF/CF，设MF=2m，则CF=3m，则CD=DF=1.5m，∴CB/CE=(MD×CF)/(CD×MF)=(DF+MF)×CF/CD×MF=(1.5m+2m)×3m/1.5m×2m=7/2，∴(CB一CE)/CE=(7一2)/2=5/2.

另，并不是BE线段不可拆，过点F作FM∥AE，交BC于M，如图

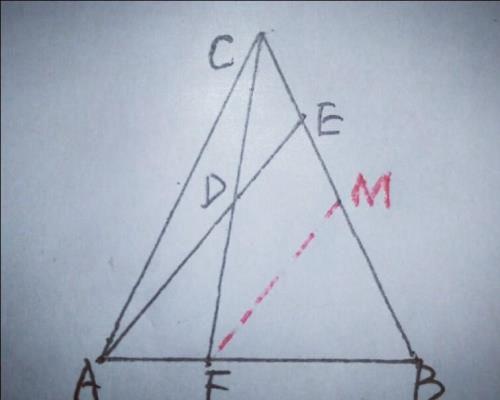
则FB/AF=MB/EM=3/2，(MB+EM)/EM=(3+2)/2=5/2，由于D是CF的中点，∴CE=EM，而MB+EM=BE，∴BE/CE=5/2.

技巧三.过一边上的点作平行线构造相似三角形

3.如图，在△ABC中，AB>AC，在边AB上取一点D，在AC上取一点E，使AD=AE，直线DE和BC的延长线交于点P，求证:BP/CP=BD/EC.

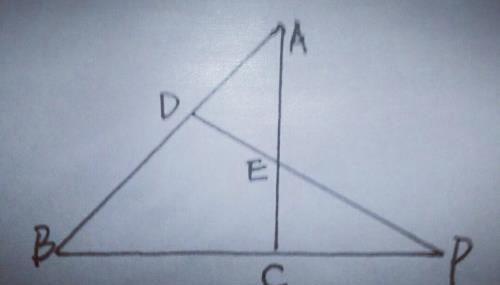
【分析】由于要证BP/CP=?，一般不破坏线段的情况下，可过C点作与BP邻边的平行线，再充分利用AD=AE这一条件，看能否证出.过C作CM∥AB交DP于M，如图

则△BPD∽△CPM，∴BP/CP=BD/CM，而CM∥AB，∠1=∠2，又∠3=∠4，由于AD=AE，∴∠1=∠3，∴∠2=∠4，∴EC=CM，∴BP/CP=BD/EC.同样过C点作CM∥DP交AB于M，也可证出如图，同学们自己证一下.

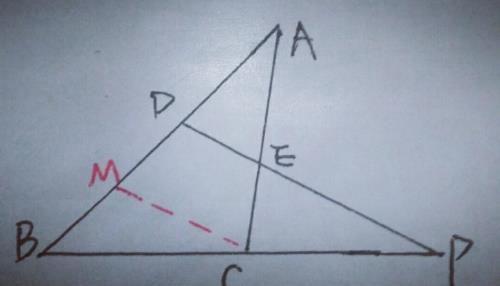
技巧四.过一点作平行线构造相似三角形

4.如图，在△ABC中，M为AC的中点，点E为AB上一点，且AE=AB/4，连接EM并延长交BC的线长线于D，求证BC=2CD.

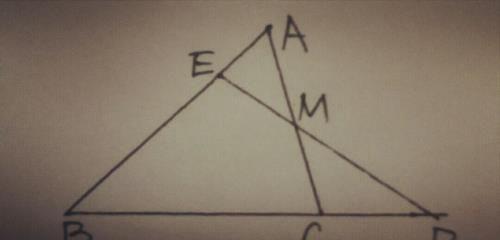
【分析】欲证BC=2CD，也即CD/BC=1/2，过C点作CF∥BE交ED于F，则△DCF∽△DEB，如图

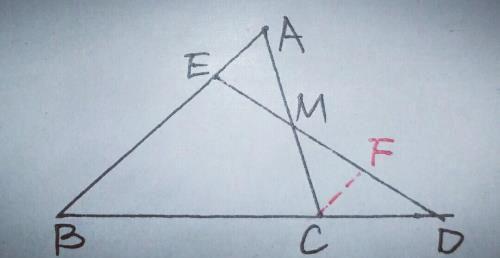
∴CD/BD=CF/BE，∵M为AC的中点，易证△AEM≌△CFM，∴CF=AE=AB/4，∴CF=AE=BE/3，∴CD/BD=CF/BE=1/3，∴CD/BC=1/2，即BC=2CD.

另，过C点作CF∥DE交AB于F，如图

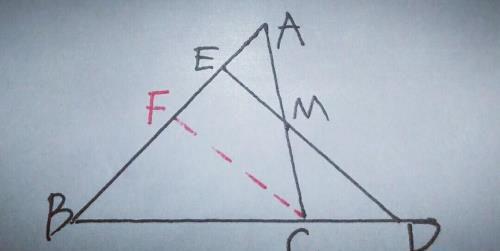
【分析】由CF∥DE，可得BC/BD=BF/BE，而M为AC的中点，则可得AE=EF，又AE=AB/4，∴BC/BD=BF/BE=2/3，∴BC/(BD一BC)=2/(3一2)，即BC/CD=2，∴BC=2CD.

另，过E作EF∥BD交AC于F，如图

【分析】由于EF∥BD，则可得EF/BC=AF/AC=AE/AB=1/4，而M为AC的中点，AF=FM，∴EF/CD=FM/CM=1/2，即EF=CD/2，由EF/BC=1/4，可得BC=2CD.

另，过A作AF∥BD交DE的延长线于F，如图

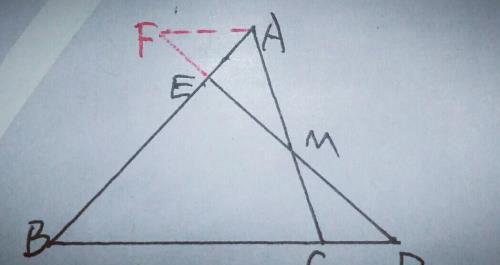
【分析】

∵AE=AB/4，∴AE/BE=1/3，由AF∥BD，可得AF/BD=AE/BE=1/3，而M是AC的中点，可证△AMF≌△CMD，∴AF=CD，∴CD/BD=1/3，则CD/BC=1/2，∴BC=2CD.

另，过A点作AF∥ED，交BD的延长线F，

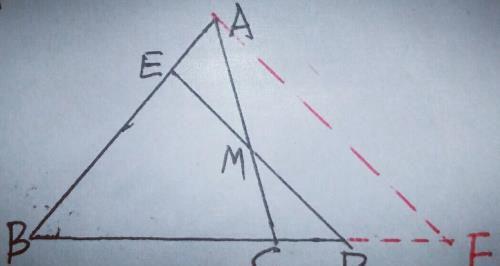
【分析】由于M为AC的中点，∴D为CF的中点，即CD=DF，又BE/AB=BD/BF=3/4，∴BD/(BF一BD)=3/(4一3)，即BD/DF=3，也就是BD/CD=3，则BC=2CD.

【总结】作平行线构造相似三角形，是常用的方法，通过一题多解，体会辅助线的好处，以及怎样作辅助线解题更简洁，同时体会有些比例关系不明朗时，可设未知数表示线段，使比例关系明朗，清晰.

感谢大家的关注、转发、点赞、交流！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小美创作整理编辑！