线性不可分是什么意思(线性可分和线性不可分区别)

导语：PLA：从线性可分到线性不可分的演化过程

从线性可分到线性不可分

PLA 从线性可分到线性不可分，有 3 种不同的形态。

线性可分：PLA

一点点错误：Pocket Algorithm

严格非线性：Φ(X)​ + PLA

接下来，详细解释下，这三种模型如何而来。

PLA 的演变过程

PLA 全称是 Perceptron Linear Algorithm，即线性感知机算法，属于一种最简单的感知机（Perceptron）模型。

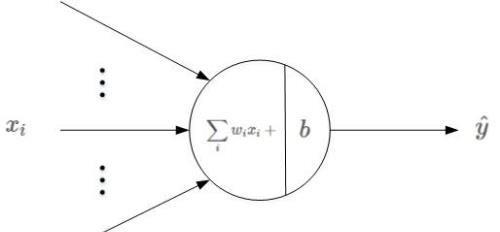
感知机模型是机器学习二分类问题中的一个非常简单的模型。它的基本结构如下图所示：

其中，xi 是输入，wi 表示权重系数，b 表示偏移常数。感知机的线性输出为：

其中，y= {+1, -1}。简单来说，它由线性得分计算和阈值比较两个过程组成，最后根据比较结果判断样本属于正类还是负类。

1. PLA 分类的原理

对于二分类问题，可以使用感知机模型来解决。PLA 的基本原理就是逐点修正，首先在超平面上随意取一条分类面，统计分类错误的点；然后随机对某个错误点就行修正，即变换直线的位置，使该错误点得以修正；接着再随机选择一个错误点进行纠正，分类面不断变化，直到所有的点都完全分类正确了，就得到了最佳的分类面。

利用二维平面例子来进行解释，第一种情况是错误地将正样本 ( y = 1) 分类为负样本 ( y = -1 )。此时，wx < 0​，即 w 与 x 的夹角大于 90 度，分类线 L 的两侧。修正的方法是让夹角变小，修正 w 值，使二者位于直线同侧：

修正过程示意图如下所示：

第二种情况是错误地将负样本 ( y = -1) 分类为正样本 ( y = 1 )。此时，wx > 0​，即 w​ 与 x 的夹角小于 90 度，分类线 L 的同一侧。修正的方法是让夹角变大，修正 w​ 值，使二者位于直线两侧：

修正过程示意图如下所示：

经过两种情况分析，我们发现 PLA 每次 w​ 的更新表达式都是一样的：w : = w + yx​。掌握了每次 w​ 的优化表达式，那么 PLA 就能不断地将所有错误的分类样本纠正并分类正确。

2. Pocket Algorithm：允许一点错误

为了避免上面线性不可分的情况，将PLA的条件放宽一点，不再要求所有的样本都能正确的分开，而是要求犯错误的样本尽可能的少，即将问题变为了：

也就是说去寻找一条犯错最少的线或者超平面。

其实，从实际意义上，是不能的，这是一个 NP hard 问题，因为线有无穷多个。无法求出最优解，因此只能求尽可能接近其最优解的近似解，这种方法被称为 Pocket Algorithm，口袋算法。

口袋算法属于贪心的思想，它总是让遇到的最好的线或超平面拿在自己手里。

简单介绍一下：首先，我们有一条分割线 w(t)​，将数据实例不断带入，发现数据点 ​(x_n,y_n)​ 在上面出现错误分类，那么我们就纠正分割线得到 w(t+1)​，如果 w(t+1)​ 犯的错误少，就将 ​w(t+1)​ 放到口袋里，否则 w(t)​ 不变。

那么如何让算法停下来呢？

由于口袋算法得到的线越来越好 (PLA 就不一定了，PLA 是最终结果最好)，所以我们就自己规定迭代次数。

Pocket Algorithm 与 PLA 相比？

线性可分的情况下：PLA 更好。先不说 PLA 可以找到最好的那条线，单从效率上来说，PLA 也更好些，最主要的原因是，Pocket Algorithm 每次比较的时候，都要遍历所有的数据点，且两个算法都要遍历一遍，才会决定那个算法好，而这还是比较一次，如果我们让他迭代 500 次的，那就麻烦了。

线性不可分的情况下：如果线性不可分，只能用 Pocket Algorithm，因为 PLA 根本不会停下来（而且 PLA 的 w(t)​ 也不是每更改一次效果就会比之前的好）

总结

Pocket Algorithm 事先设定迭代次数，而不是等着算法自己收敛到最优。随机遍历数据集，而不是循环遍历。遇到错误点校正时，只有当新得到的 w 对于所有的数据优于旧 w 的时候（也就是整体错误更少的时候）才更新，而 PLA 算法中，只要出现错误分类就更新。由此也可知，pocket Algorithm 算法是保证每次得到的线或平面面是越来越好的，而 PLA 算法不一定。而且，由于Pocket 要比较错误率，需要计算所有的数据点，因此效率要低于 PLA。所以在线性可分的数据集上，使用 PLA 算法，而不选择使用 Pocket 算法。但是，只要迭代次数足够多，Pocket 和 PLA 的效果是一样的，都能够把数据完全正确分开，只是速度慢。3. 线性可分到线性不可分

PLA 的非线性可分类似 SVM 的对偶问题一样，在所有 w​ 和 b 的更新中，假设 xi​ 点贡献了 ni 次，令 αi = niη，则 w, b​ 可表示为：

所以感知机的模型又可以表示成：

将 PLA 的输入空间通过核函数映射到高维，实现线性可分。

本文内容由小馨整理编辑！