霍夫曼编码压缩率怎么算(霍夫曼编码压缩文件)

导语：每天一个算法——霍夫曼编码压缩算法

算法是自己作为程序员开发比较薄弱的地方，之前大学的时候也没有好好学，工作中具体用到的也很少。但我深知算法是程序员这个行业，真正有意义的地方，搬砖似得码农到处都有，但如果你会点算法，可能一次可以搬两块砖也说不定。所以，我决定今天起，开始认真整理和算法相关的一些东西，作为自己的一点成长，一点积累。也欢迎大家关注我，一起讨论，一起进步。

霍夫曼编码压缩算法，是数据压缩中经典的一种算法。这是一种根据文本字符出现的频率，重新对字符进行编码，频率越高的词，编码越短，从而达到数据压缩的效果。

假设我们有这样的一段数据需要进行编码——“beep boop beer!”。这段字符通过ASCII编码后的结果为62 65 65 70 20 62 6F 6F 70 20 62 65 65 72 21 （十六进制），总共有十五个字节。

首先，我们先计算每个字符出现的频率，经过我们统计，得到下面一张表：

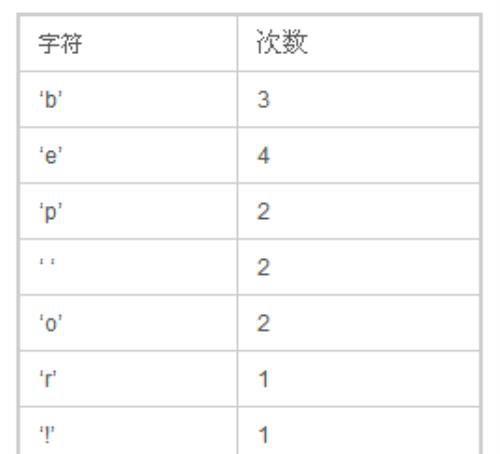
然后把这些数放到优先级队列中，从左到右，频率逐渐增加。

下面我们需要把这个队列，转换成霍夫曼二叉树，这是一个带有权重的二叉树，在队列中每个字符出现的次数，标识这个字符的权重，霍夫曼二叉树始终保证权重高的在越高的地方。下面来介绍，二叉树是如何演变的。

我们从最左边开始，取两个元素来构造一个二叉树（第一个元素是左结点，第二个是右结点），并把这两个元素的权重相加，得到新的空元素。

同理，我们继续取最左边两个元素，进行权重相加（2+2=4），相加结果变大，需要对权重进行重新排序。

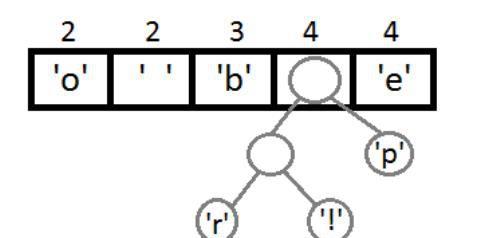
继续执行同样的操作，这里可以看到自底向上的构建二叉树的一个过程。

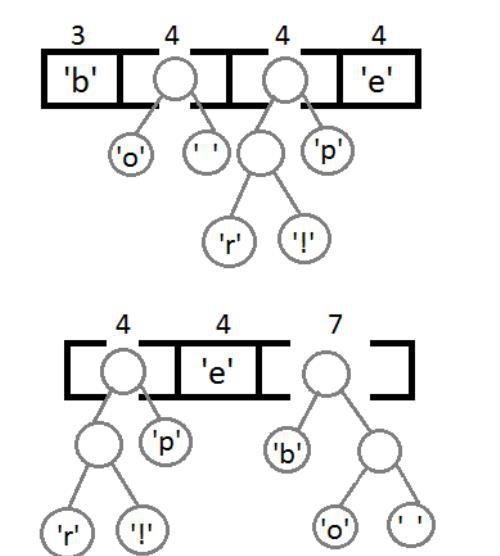
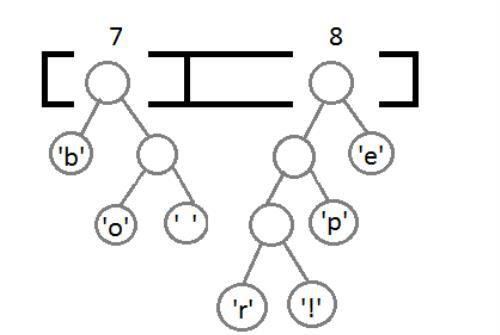
最后，我们得到这样一个带有权重的二叉树：

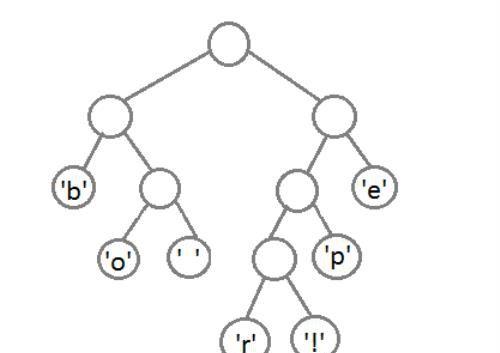
这里，我们把这个树的左边分支用0编码，右边分支用1，这样我们就可以遍历这棵二叉树获取每个字符的编码，例如：‘b’的编码是 00，’p’的编码是101， ‘r’的编码是1000。我们可以发现出现次数越多的字符会越在上层，它的编码也越短，次数少的字符，编码越长。

最后我们可以得到下面这张编码表：

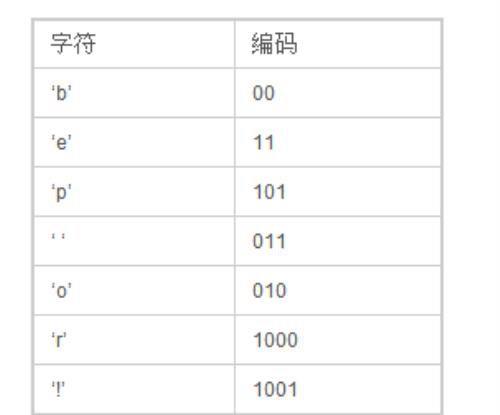
利用这个编码表我们对字符串“beep boop beer!”重新进行编码，得到：0011 1110 1011 0001 0010 1010 1100 1111 1000 1001。共计40位二进制，而之前没重新编码时，是15字节共120位，这样看来压缩比例还是比较客观的。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小德创作整理编辑！