求四边形面积的题型(小升初求四边形面积)

导语：一道初中几何题-求四边形的面积

一道初中几何题-求四边形的面积

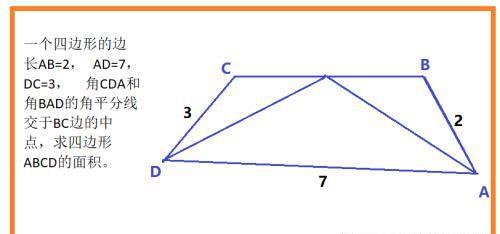
一个四边形的边长AB=2， AD=7， DC=3， 角CDA和角BAD的角平分线交于BC边的中点，求四边形ABCD的面积。

解： 如图， 设BC的中点为M，有M做AD的垂线，取DP=DC， AQ=AB，

根据角分线的关系有∠CDM=∠PDM， DM为公共边，且DC=DP， 所以

三角形CDM全等于三角形DPM， 因而MC=MP，

∠MPD=∠C，∠CMD=∠PMD

同理三角形BAM全等于三角形QAM, 因此 MB=MQ，

∠MQA=∠B，∠BMA=∠QMA

由此推出MP=MQ

因此∠MPD=∠MQA=∠B

这说明四边形MPAB四点共圆。

所以∠CMP=∠BAP，

由此得出DMP=∠MAQ， 此外∠MPD=∠AQM，因此

△MDP相似于△AMQ

所以：MP/QA=DP/MQ

但MP=MQ， 即

MP·MP=QA·DP=2x3=6

因为PQ=7-2-3=2， 则PS=1，

利用勾股定理：

即高MS=√（6-1）=√5

如MU和MV分别是DC和AB的高，则MU=MV=MS=√5

四边形ABCD的面积=三角形CDM的面积+三角形MDA的面积+三角形ABM的面积

=（3√5）/2+（7√5）/2+（2√5）/2

=6√5

本文内容由小馨整理编辑！