不等式利润问题(soap怎么读啊)

导语：中考数学方程思想的运用——不等式中的利润问题（四）

某蔬菜加工公司先后两批次收购蒜薹（tai) 共100吨。第一批蒜薹价格为4000元／吨；因蒜薹大量上市，第二批价格跌至1000元／吨，这两批蒜薹共用去16万元。

（1) 求两批次购进蒜薹各多少吨？

（2) 公司收购后对蒜薹进行加工，分为粗加工和精加工两种，粗加工每吨利润400元，精加工每吨利润1000元。要求精加工数量不多于粗加工数量的三倍。为获得最大利润，精加工数量应为多少吨？最大利润是多少？

分析：（1）由题意可知第一批与第二批一共100吨，并且一共用了160000元，所以可用二元一次方 程列式解答。

（2）又涉及到利润问题，一般的都是依据公式（总利润=单个利润X数量）来列式。此题可以 将总利润表示出关系式，然后结合限定条件（精加工数量不多于粗加工数量的三倍）来 讨论得出最终结果。

过程：解 （1）设第一批蒜薹x吨，第二批蒜薹y吨。 由题意得：

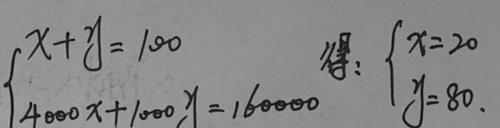
答：第一批蒜薹20吨，第二批蒜薹80吨。

（2）设精加工的有a吨，则粗加工的有（100-a）吨；总利润为w元。

答：精加工为75吨时，获得最大利润，最大利润是85000元。

一次不等式的应用问题，是历年中考的必考题型。经常与函数（一次和二次函数）的图像性质（增减性、对称轴、自变量取自范围等）相结合。解决此类问题要抓住题目要点（得出自变量范围），结合函数图像性质，确定结果。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小姬创作整理编辑！