无理点处连续有理点间断(有理点连续无理点不连续的函数)

导语：数学奇谈：一个在有理点间断，无理点连续的函数！

在我们的印象中，一般初等函数都是连续的，比如

f(x)=x，平面上一条45度角的直线

f(x)=1/x，分布在第一和第三象限的对称曲线，与坐标轴无限接近

f(x)=sinx，三角函数，周期为2Pi

如此，等等。

但是随着数学的发展，尤其是到了近代，越来越多“奇怪”的函数被发现，或者说被构造出来。这些在大众看来“不可思议”、“毫无意义”的函数，在数学中常常用来构建反例。

这期数学奇谈，就给大家分享一个这样的函数（原例见周民强编著《实变函数》，本文补充了证明过程）：在有理点间断，但在无理点连续。（一般情况下，如一开始举例的那类函数，如果在有理点间断，由于区间内的有理点数量无穷，在实轴上稠密，势必就不存在连续点了）

构造函数：在开区间（a，b）上取全体有理点集，记作{rn}（n是下标），如下

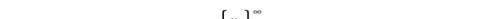
（a，b）上有理数集

然后作一个分项为正值的收敛级数，如下

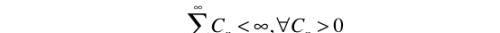
如此定义（a，b）上的函数f(x)

大家可以验证，f(x)是单调递增函数。我们接下来验证f(x)在有理点间断，在无理点连续。

一、在有理点间断

当x > rn时，f(x)对应的累加项中包括Cn；当x < rn时，f(x)对应的累加项中不包括Cn。于是至少有下式

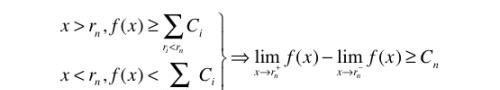
所以，f(x)在全部有理点都间断。

二、在无理点连续

任意取（a，b）上无理数x0，于是有如下关系

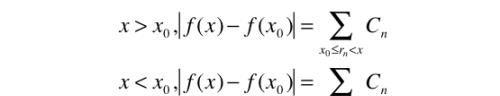
其中，x属于（a，b）

我们先看看x>x0的情形：反证法，假设右侧不连续。则存在ε > 0,对于任意σ > 0,都有y满足如下关系

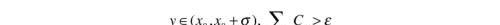
于是我们可以作如下构造：

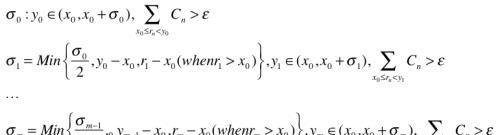
σ0 > 0

上述构造中，“when rm > x0”是一个假设项。即，若rm > x0，则取ym时要在rm的左侧取值；若rm < x0, 则无需理会此假设项。我们的目的是按照自然数次序把rm剔除出去。

这样，ym单调递减趋于x0，且有如下关系

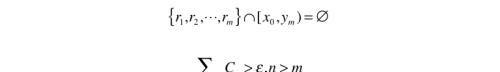
这与级数收敛相矛盾，所以f(x)右连续。利用同样的手法，可以证明f(x)左连续。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小春创作整理编辑！