c语言数据结构二叉树的基本操作(c语音二叉树)
导语:C语言:数据结构-二叉树的定义和基本术语和二叉树的性质
(1)二叉树的定义
二叉树(Binary Tree):每个结点至多有两棵子树,且子树有左、右之分。在二叉树中不含度数大于2的结点。
二叉树的递归定义为:二叉树或者是一棵空树,或者是一棵由一个根结点和两棵互不相交的分别称作根的左子树和右子树所组成的非空树,左子树和右子树又同样都是一棵二叉树。
(2)二叉树的基本术语
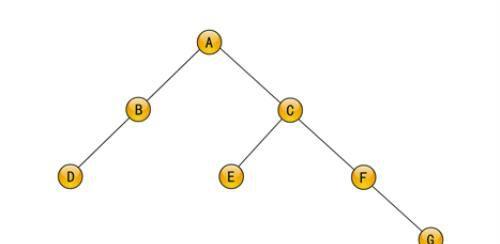
如图6-4所示的一棵二叉树BT,它由根结点A和左子树BT1及右子树BT2所组成,BT1位于A结点的左下部,BT2位于A结点的右下部;BT1又由根结点B和左子树BT11(它只含有根结点D),右子树BT12(此为空树)所组成;对于BT2树也可进行类似的分析。
1.左孩子:结点的左子树的根。如在图6-4的二叉树BT中,A结点的左孩子为B结点,B结点的左孩子为D结点。
2.右孩子:结点的右子树的根。如在图6-4的二叉树BT中,A结点的右孩子为C结点;C结点的右孩子为F结点。
二叉树BT
3.满二叉树
在一棵二叉树中,当第i层的结点数为2i-1时,则称此层的结点数是满的,当树中的每一层都满时,则称此树为满二叉树。
图6-5(a)为一棵深度为4的满二叉树,其结点数为15。图中每个结点的值是用该结点的编号来表示的。对一般二叉树,其结点的顺序编号规则为:树根结点的编号为1,然后按照层数从小到大、同一层从左到右的次序对每个结点进行编号,若双亲结点的编号为i,则左、右孩子结点的编号分别为2i和2i+1。
满二叉树和完全二叉树
4.完全二叉树
在一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在最右边缺少连续若干个结点,则称此树为完全二叉树。
由此可知,满二叉树是完全二叉树的特例。图6-5(b)为一棵完全二叉树,它与等高度的满二叉树相比,在最后一层的右边缺少了5个结点。该树中每个结点上面的数字为对该结点的编号。
5.理想二叉树
与完全二叉树类似的一个概念为理想二叉树,它是在对应的满二叉树的最下一层中的任何位置缺少结点或不缺少结点。如在图6-5(a)的满二叉树的最底层缺少编号为10、13、14等3个结点,则构成一棵深度为4的理想二叉树。
由此可知,理想二叉树包含满二叉树和完全二叉树在内,也就是说,一棵满二叉树或完全二叉树必然是一棵理想二叉树,反之,一棵理想二叉树不一定是一棵满二叉树或完全二叉树。
二叉树的性质二叉树上终端结点数等于双分支结点数加1
设二叉树上终端结点数用n0表示,单分支结点数用n1表示,双分支结点数用n2表示,则总结点数为n0+n1+n2;另一方面,在一棵二叉树中,所有结点的分支数(即度数)应等于单分支结点数加上两倍的双分支结点数,即等于n1+2n2。由树的性质可得:
n0+n1+n2=n1+2n2+1 即n0=n2+1
例如,在图6-4的二叉树BT中,度为2的结点数为2个,即A和C,度为0的结点数为3个,即D、E、G,它比度为2的结点数正好多1个。
二叉树上第i层上至多有2i-1个结点(i≥1)由树的性质2可知:度为k的树中第i层上至多有ki-1个结点。对于二叉树,树的度为2,将k=2代入ki-1即可得到此性质。
深度为h的二叉树至多有2h-1个结点由树的性质3可知:深度为h的k叉树至多有(kh-1)/(k-1)个结点。对于二叉树,树的度为2,将k=2代入(kh-1)/(k-1)即可得到此性质。
对一棵二叉树中顺序编号为i的结点,若它存在左孩子,则左孩子结点的编号为2i;若它存在右孩子,则右孩子结点的编号为2i+1,若它存在双亲结点(即编号不等于1),则双亲结点的编号为[i/2]完全二叉树中,对于编号为2的结点,其左孩子结点的编号为4,右孩子结点的编号为5,双亲结点的编号为1;对于树中的其他结点也可进行类似的分析。由于该树的结点的最大编号为10,所以分支结点的最大编号为5。
具有n个结点的理想二叉树的深度为[log2(n+1)]或[log2n]+1此性质可以从树的相应性质中直接导出,也可以进行如下证明。
证明:设所求理想二叉树的深度为h,由理想二叉树的定义可知,它的前h-1层都是满的,最后一层可以满,也可以不满,由此得到如下不等式:
2h-1-1<n≤2h-1
可变换为: 2h-1<n+1≤2h
取对数后得: h-1<log2(n+1)≤h
即: log2(n+1)≤h<log2(n+1)+1
因h只能取整数,所以: h=log2(n+1)
完全二叉树的深度h和结点数n的关系,还可表示为:
2h-1≤n<2h
取对数后得: h-1≤log2n<h
即: log2n<h≤log2n+1
因h只能取整数,所以: h=log2n+1
如对于图6-5(b)所示的完全二叉树,n=10,log211等于log211+1,其值为4。
本文内容由小曲整理编辑!