仿射变换的矩阵(什么是仿射变换用矩阵形式如何表示仿射变换)

导语：矩阵变换—仿射变换和齐次坐标

[Tip]: 齐次向量[x y z w]T ，w = 0时，该齐次向量表示一个点。w = 0时，则表示向量。

仿射变换

1.缩放变换和旋转变换称为线性变换（linear transform）

2.线性变换和平移变换统称为仿射变换（affine transfrom）

3.投影变换所用到的变换则称为射影变换

齐次坐标

1.齐次坐标是用N + 1个数来表示N 维坐标的一种方式。

2.如三维矩阵无法通过右乘进行平移变换，将三维坐标扩展成四维齐次坐标。

2D矩阵

通过上图，可以构建如下矩阵：

3D矩阵

缩放

三维空间的缩放可以用3X3的矩阵 M_scale 表示(1-1)：

1.scaleX ，scaleY ，scaleZ 分别表示沿着x，y，z轴方向上的缩放系数。如果全部缩放系数都相等， 那么该缩放操作称为均匀缩放，否则，称为非均匀缩放。

2.Unity中使用列向量和列矩阵描述顶点信息，所以可以把顶点坐标右乘缩放矩阵实现缩放操作。

旋转

1.在Unity里面，我们约定旋转顺序是先Z轴，再X轴，最后Y 轴，但是由于我们旋转会导致向量基方向变化，所以如果按照上面的顺序是有问题的，所以只要反过来写：先Y 轴，再X轴，最后Z轴。

2.要定义一个旋转操作，需要定义对应的旋转轴。当某向量分别绕着坐标系的xyz旋转θ角度时，分别 用以下旋转矩阵Mr_x ,Mr_y ,Mr_z 表示：

代码举例：自定义灯光旋转

构建旋转矩阵

构建灯光

平移

与缩放旋转不同，平移是一个加法操作。平移变换不是一个线性操作。

因为用右乘一个三阶矩阵实现对一个三维向量进行平移变换是不可能实现的。要解决这个问题，需要使用齐次坐标。

将三维向量[x y z]T 扩展成一个四维其次坐标[x y z w]T 。将平移向量扩展成为四阶矩阵的形式。

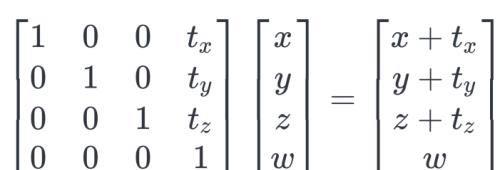
旋转与缩放矩阵也可以通过增加第4列与第4行的方式将矩阵四阶化。

仿射变换的原理就在这里了，有问题欢迎大家指正。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小春创作整理编辑！