从定义理解散度的含义是什么(从定义理解散度的含义有哪些)
导语:从定义理解散度的含义
先看通量定义:

图1
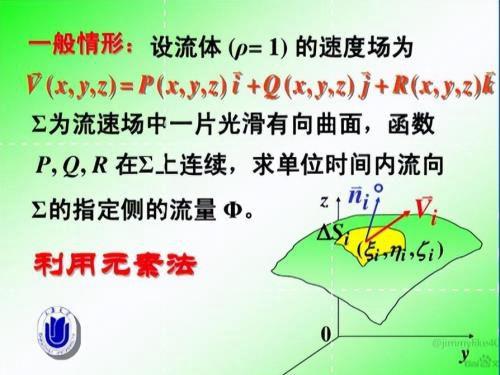
图2
上面的定义很简单,也很好理解,那就是速度为v的流体流过一个曲面的流量就是通量。
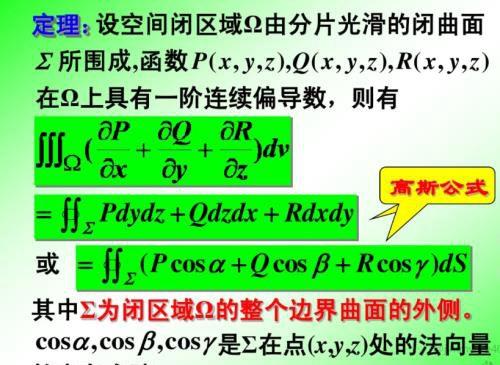
图3
上图的高斯公式的意思是,通过曲面积分计算出来的通过一个闭合曲面的通量,等于通过
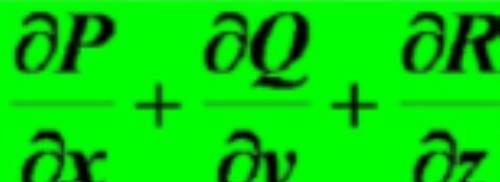
这个函数对于这个曲面所围成的立体进行体积分。那么,这个函数是什么呢?

图4

图5
由上面定义,我们看到,上面的那个函数就是散度。
由于通过空间中一个没有大小的点的流量很难理解,这里提出如下方法:
要理解散度的意义,先要理解Δv的意义。Δv是一个包含无穷小体积的闭合曲面。那如何理解这个无穷小的体积呢?
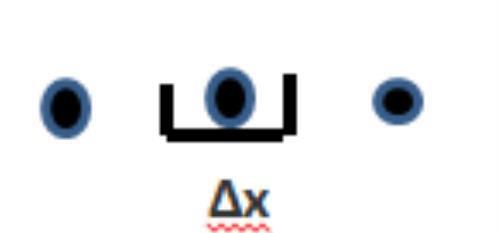
图6
我们知道,任意两个不同的数字之间必然存在着差值,而任何一个确定的数字都对应着数轴上的一个点,现在我们假设图6是数轴上间隔任意小的三个点,但不管它们之间的间隔多小,只要它们不相同,就必然存在间隔。这个时候我们就可以假设,用一个长度为Δx的篮子装下数轴上的一个点,这个篮子的长度比数轴上任意两个点之间的间隔都要小,也就是我们所说的无穷小,也就是它的长度无法用任何一个确定的数字表示,但它又比0大,所以它能装下一个大小为0的数字,而且只能装下一个点,如果能装下两个点,而两个点对应两个确定的数字,它们之间也就必然存在可以用确定的数字表示的间隔,那就不是无穷小。
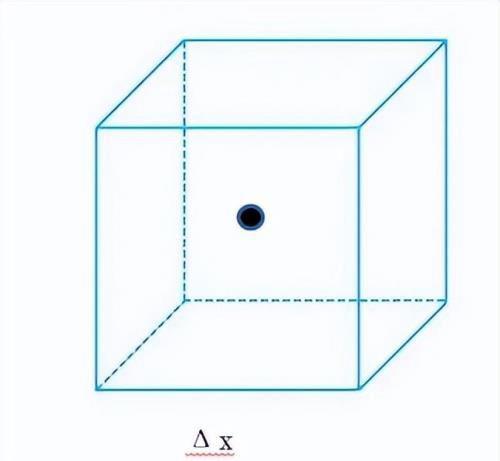
图7
按照上述假设,我们可以假设上图长度为Δx的立方体只能装下空间中的一个点,这就是图4定义中Δv的含义。通过建立边长无穷小的立方体,就可以理解散度定义的意义:散度就是流体通过空间中某一个点的通量与体积之比。
按照上述解释,散度就是通过图7立方体的流体的流量和这个立方体体积的比率。
那么,这个比率代表什么意思呢?
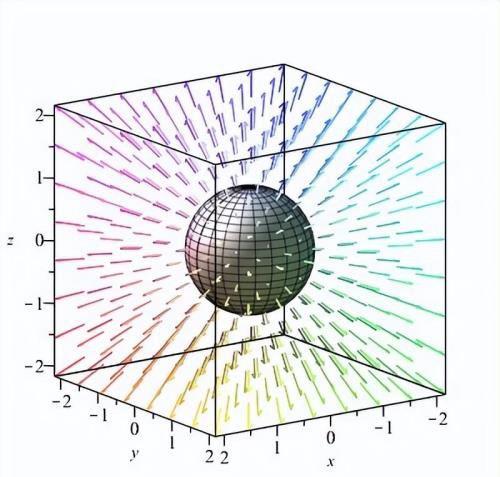
图8
我们假设上图的立方体由无数个图7的无穷小的立方体构成,这些立方体的体积是一样的,都是Δv,而流过这些立方体的流体的流量
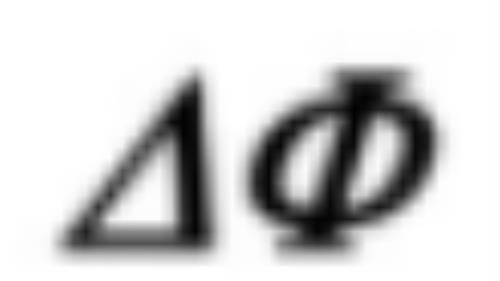
是变化的,可以由图4的公式看出来:
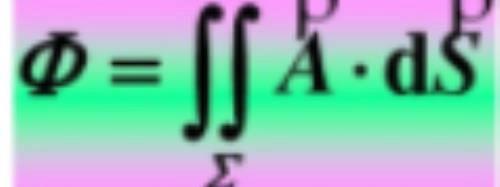
这里的A代表流体速度,参考图1,这个速度是一个关于x,y,z的函数,也就是空间每个点的流体的速度都不一样,从而导致相同的Δv,比值
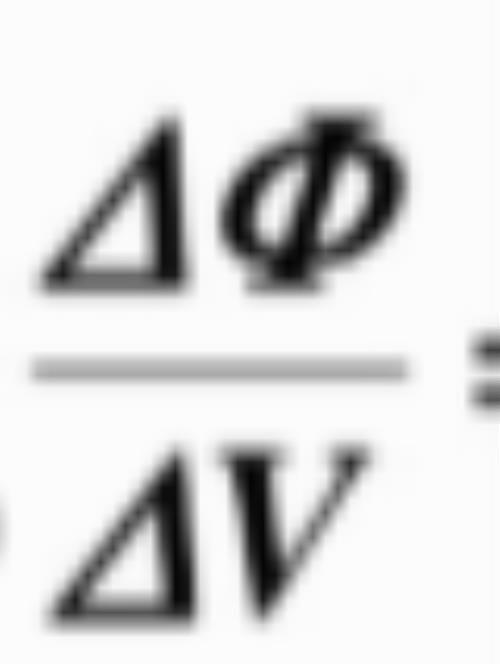
不一样。所以,图8的空间中每一点不同的散度,反映的其实是每个点不同的流体的速度。那么,流体的速度又代表什么呢?
流速是单位时间内流体通过某一截面的平均速度:
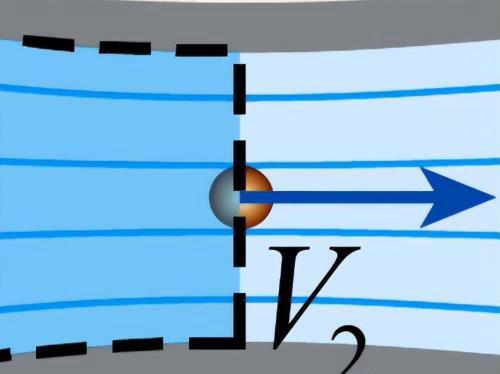
按照上述理解,假设图8的中心球体是一个灯泡,由于灯泡发出的光会随着距离变大而减弱,我们这里认为是光线的数量减少,所以通过空间中不同距离的两个相同的立方体的光线数量肯定不同,也就是流量
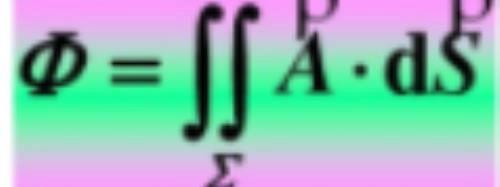
不同。这里可以认为单位时间内流过立方体的光线数目就是流体的速度。
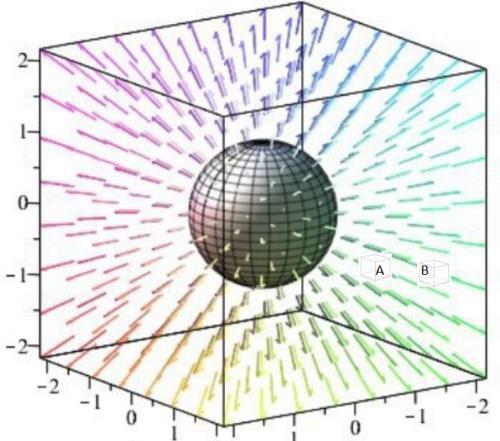
图9
上图是在图8中放入两个图7一样的无穷小的立方体。由于A、B两点距离球心灯泡的距离不同,所以散度值也不一样。假设通过A的光线是100根,通过B的光线是50根,看起来就像是随着距离的增加光线散开了一样,这大概就是散度这个名称的由来。
另外,由散度表达式

也可以看到,按图2,因为P、Q、R代表的是流体速度在三个坐标方向的分量,对它们分别在三个方向求导数,表示的就是这个流体速度相对于空间距离的变化率。
这个流体速度的变化率在图9的例子中就可以认为是不同距离通过相同立方体的光线数目的变化。
因此,导数求出的是一条曲线上每一个点的斜率,散度求出的则是空间上每一个点的流体速度相对于空间距离的变化率。
大概总结一下:
1:散度首先是一个标量,是一个数字,是流体速度变化率。
2:通过建立只包含空间一个点的边长无穷小的立方体,便于理解散度的概念。
3:对于流体、光线、磁力线等等,散度值对于空间中不同的点是会变化的。
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小梓创作整理编辑!