角格点问题一般解法(角格点经典例题)

导语：一道“角格点”经典好题的求解“说三法”

平面几何中的“角格点”问题，既有难度、又有趣味；既有规律、又有技巧；外形简精明了、内含丰富知识；今举经典好题一例，说说其的三种思路：

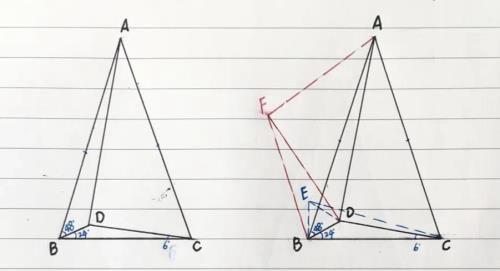
【例题】（如图）在△ABC中，点D为其内一点，且：AB=AC，∠DBA=48º，∠DBC=24º，∠DCB=6º，求：∠BAD的度数

【思路一】（造全等、作共圆、找外心）

（1）已得：∠BAC=36º，∠BCA=∠CBA=72º，

（2）由∠BDC=150º，以BD为边作正△BDE，连EC，易证△DCB≌△DEC（SAS）∴BC=EC，∠DCB=∠DCE=6º，即：∠BCE=12º

（3）以AB为底作等腰△ABF，使FA=FB，连接FD，∴∠FAB=∠FBA=36º，则：∠FBC=108º，∠FAC=2×36º=72º

（4）所以：A.F.B.C四点共圆，∴BF=BC=FA

（5）容易证得：△FBD≌△CBE（SAS），∴FD=CE=BC=FB，∠BFD=∠BCE=12º

（6）由FB=FD=FA，∴点F为△ABD的外心，得：∠BAD=∠BFD/2=12º/2=6º

【思路二】（正弦定理、找相似形）

（1）由已知得：∠BAC=36º，∠BCA=72º

（2）作∠ABD的平分线交CD的延长线于点E，∴∠EBD=24º，∠EDB=24º＋6º=30º

（3）△BDE中，得：BE/BD=sin30º/sin126º，即：BE/BD=1/2sin54º

（4）△ABC中，得：BC/AB=sin36º/sin72º，即：BC/AB=1/2cos36º=1/2sin54º

（5）则BE/BD=BC/AB，∠EBC=48º=∠DBA，∴△BCE∽△BAD，∠BAD=∠BCE=6º

【思路三】（作内心，造相似）

（1）作∠ABD的平分线交AC边于点E，则有：∠BEC=36º＋24º=60º，延长CD交BE于点H，则：∠BDH=24º＋6º=30º

（2）作∠BCE的平分线交BD的延长线于点F，则点F为△BCE的内心，连EF，则∠BEF=30º，∠BCF=36º。

（3）易证△ABE∽△CBF，∴AB/BC=BE/BF

（4）易证△BEF∽△BDH，∴BE/BF=BD/BH

（5）得：AB/BC=BD/BH，在△ABD与△CBH中，又∠ABD=48º=∠CBH，∴△ABD∽△CBH，∴∠BAD=∠BCH=6º

以上思路之分析，“道听度说”供参考。

本文内容由小彤整理编辑！