射影定理的三个证明方法(射影定理求证)

导语：射影定理证明及应用初中数学超有方向教育

射影定理在一些初中教材中已经被删除掉了，但是它真的非常好用，在一些选择填空题里不用去证明，直接拿来用秒出答案。

下面我们来看一下利用射影定理来计算证明的题型。

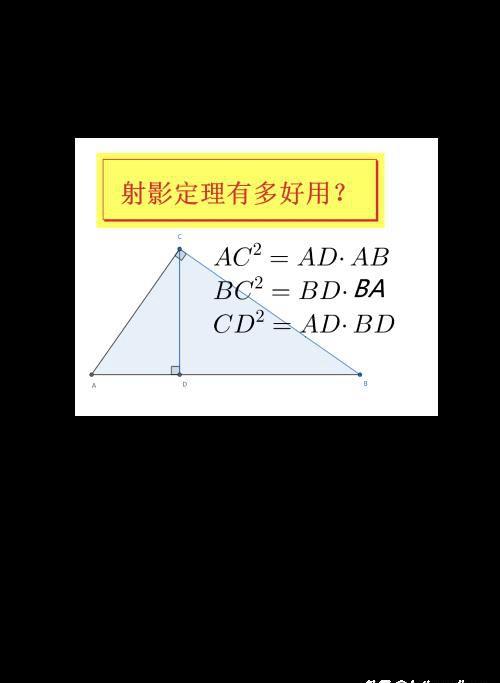
直角△ABC∠ACB=90°，CD⊥AB于D，我们就有以下结论

AC2=AD·AB CD2=AD·DB BC2=BD·AD

证明：

∵∠A=∠A

∠ADC=∠ACB=90°

∴△ACD∽△ABC

∴AC2=AD·AB

同理另外两个可证。

证明：延长BO交AE于F，BF⊥AE

连接CF，那CF也⊥AE，

因为是对折轴对称图形

或者用简单的垂径定理来证明，所以C、F、O、B就在同一条直线上

那BO=BC-CO

那我们来看一下现在就有了直角三角形CAB和它斜边上的高AF，是不是可以用射影定理啊

三个出发点用哪个呢，AC是已知的就用AC吧

AC2=CF×CB，那CB在直角三角形ABC中可以用勾股定理算出来22+42开根号=2

CF= AC2/CB=4/2

BO=BC-CO=2

解题思路，射影定理

我们先来整理一下思路

要求AF长度，AF=BE，证明等腰梯形就可以了这个很简单

BE、CE和DE刚好满足射影定理，DE2=CE×BE那DE=2，知道CE就可以了

CE：BE=CD：AB=1：2（△CDE∽△ABE）好解决了

DE2=CE×2CE，CE=

BE=

=AF

假设CE长x，BE长2x，那么22=x·2x

本文内容由小楠整理编辑！