旋度怎么理解(旋度的概念及其物理意义)

导语：旋度的简单理解方法

转发一篇关于旋度意义的解释。

什么是旋度：假设有一速度场，旋度是度量该速度场中的旋转分量。即以数学语言的方式来形容速度场的旋转程度。

1、旋度公式：

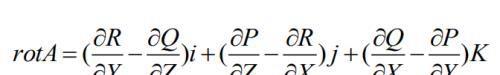
为了便于记忆将公式写成：

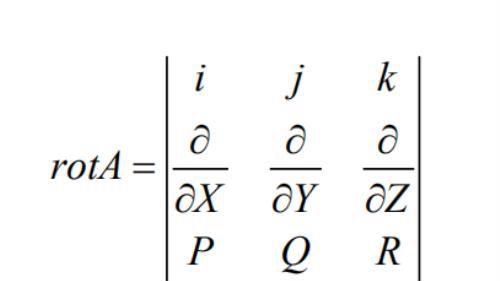
2、我们该如何理解旋度？

首先我们不考虑三维空间，建立一个二维平面，即 XY 平面。假设速度场沿 X 方向速度分量是 P（x,y）i,沿 Y 方向的速度分量是 Q（x,y）j。在 XY 平面中有一刚体。如下图：

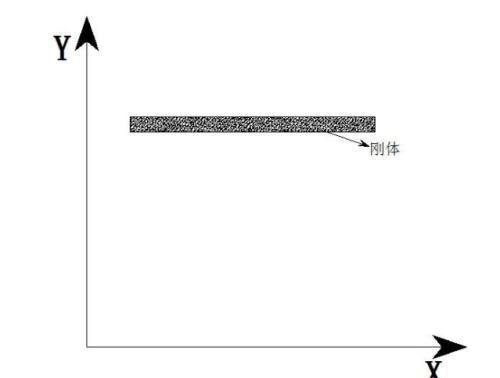
图中的刚体可以是一块木板、玻璃什么的。

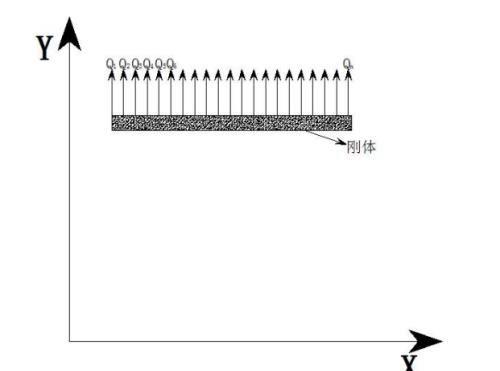
当向量 Q1=Q2=Q3=……Qn的时候，其中Q向量代表速度，向量的长度代表速度的大小。大家可以发现刚体将沿着平行于 Y 轴的方向运动，而不会发生旋转，那么我们说刚体的旋度是 0。即

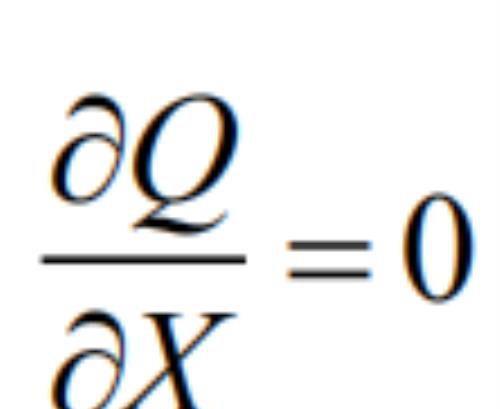
刚体将不发生旋转。那么刚体如何才能旋转呢？

大家很容易发现当

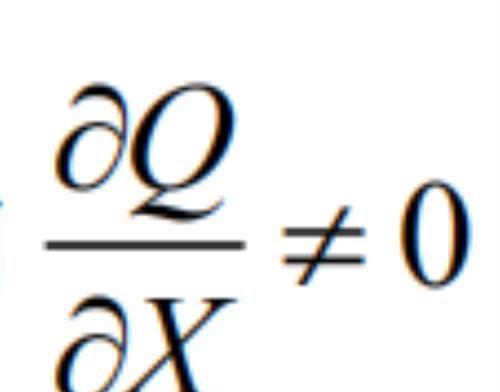
的时候，即沿着刚体的方向 Q 发生变化时候刚体将产生旋转，如下图：

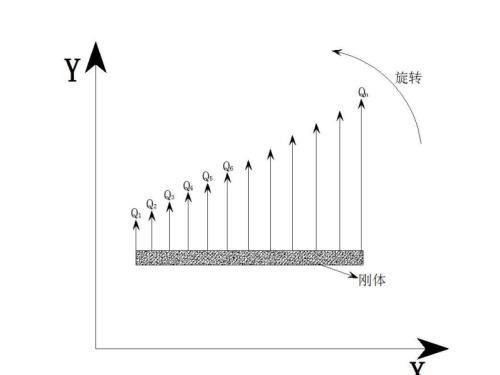
物理学中我们知道旋转线速度=角速度 半径（v=w r），所以角速度

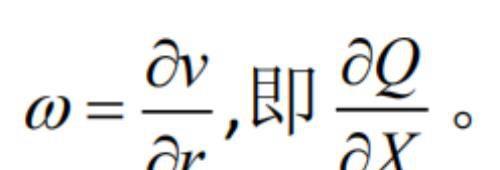
旋转轴方向垂直于 XY 平面。接下来我们看图中的 A 点，如下图：

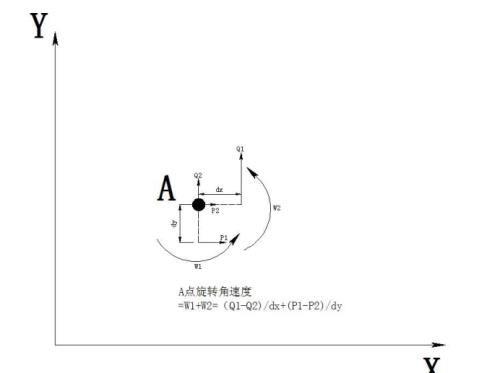
这里的P1,P2和Q1,Q2指刚体上不同的点相对于Y轴和X轴的角速度变化。

那么很容易发现该旋转是两个旋转的叠加，某一点的角速度

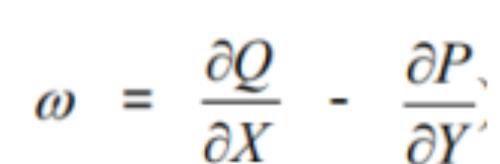
即旋度为

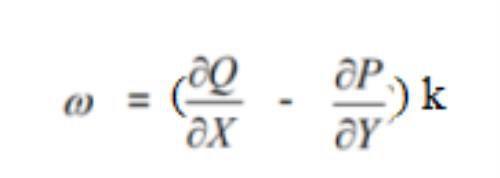
由于这是在XOY平面得出的结果，同样在YOZ、XOZ平面也可以得出同样的推论，因此得到旋度公式

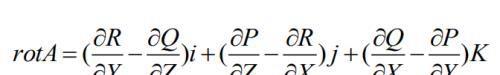
通过上面的推理大家应该已经能够差不多理解旋度的意义了。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小樊创作整理编辑！