导语：向量，射影定理，勾股定理

内积的交换律结合律

向量在直线上的投影：任意点到一直线的垂足叫该点到该线的投影点，一个向量a向另外一条直线做投影，是指向量的两个端点向该直线做投影，起始投影点到终投影点的向量叫a向量在该直线上的投影向量。

①内积交换律

内积为正的情况

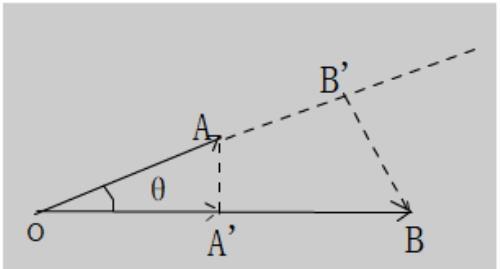
图1

内积为负的情况

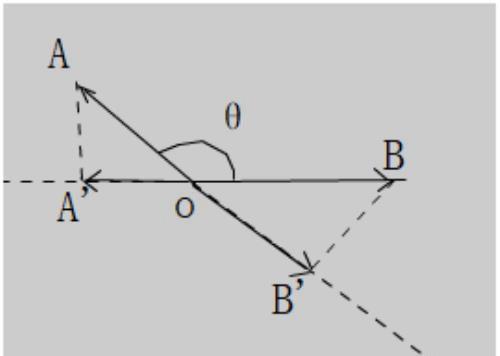
图2

两者都有⊿OAA’∽ ⊿OBB’

OA:OB=OA’:OB’=> OA·OB’= OB·OA

射影定理

射影定理：直角三角形中直角边的平方等于，该边在斜边上的射影与斜边长度的乘积。

考虑图1中，A与B'点重合的特殊情形，这时三角形OAB就是直角三角形，如图3

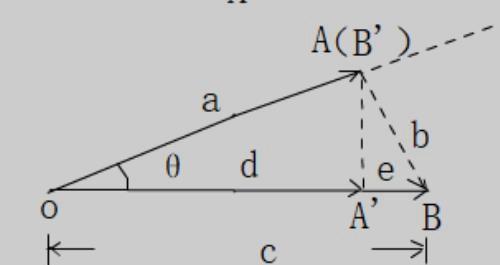
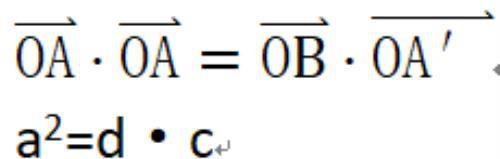
由射影定理到勾股定理

射影定理

a2=d·c

b2=e·c

勾股定理

a2+ b2=d·c+ e·c=（d+e）·c=c2

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小梓创作整理编辑！