一道求三角形边长的题(一道求三角形边长的题目及答案)

导语：一道求三角形边长的题

一道求三角形边长的题

在三角形ABC中， AB=86， AC97， 一个以A为圆心， AB长为半径的圆交于BC点X， 且BX和CX有整数长度，BC的长是多少？

解： 根据题意画出草图如下，显然AX=86，让BX=x, CX=y,

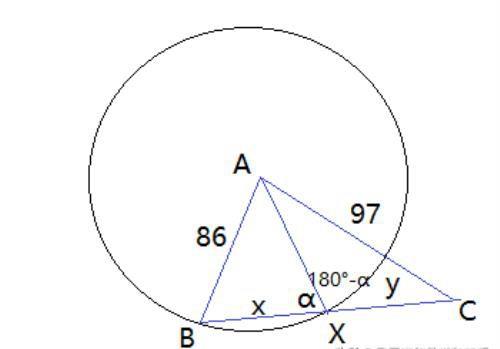
在三角形ABX中利用余弦定理：

在三角形AXC中利用余弦定理：

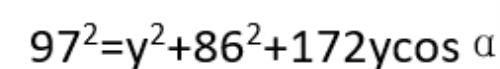
两个式子相减有：

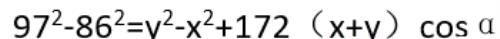
此外根据等腰三角形ABX有

cosα=x/172

带入上面的式子有：

（97+86）(97-86)=(x+y)y

即：

183x11=(x+y)y

因为x和y都是整数，现在考察y能否等于11，如果y=11, 那么因为AX=86，则有

AX+CX=86+11=97=AC，不满足三角形AXC的构成条件，即两边之和大于第三边，所以y不能等于11，

又有183x11=61x33=(x+y)y

且61是质数，所以仅有一种可能：

有y=33, x+y=61,

因此x=61-33=28,

所以BC的长度为61.

解法2：利用圆的割线定理，如下图：

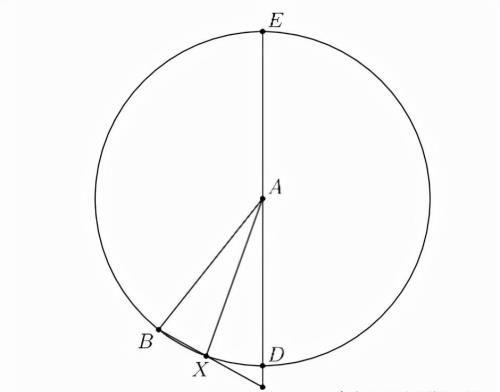
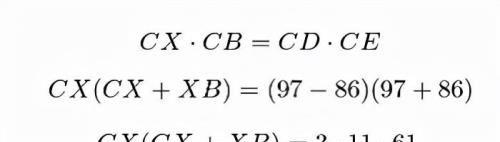
由于：

这样：

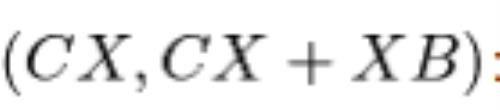
会有四对组合：

因为CX>13, 所以只有：

CX+XB=61

后记：上面提到的割线定理是初中几何中可以很容易证明的一个定理，利用两个三角形相似即可证明，参见下图。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小岑创作整理编辑！