泰勒级数的推导过程(泰勒级数怎么理解)

导语：泰勒级数推导思路的理解

图1

泰勒 ( Taylor ) 级数

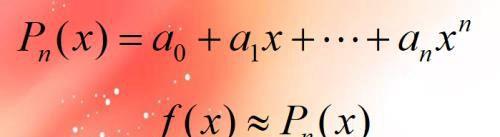
图2

图3

从图2图3可以看到，函数p(x)形式已知，现在的目的是把f(x)用p(x)的形式来表示出来。在

p(x)里面，系数ai是未知的。同时，要把f(x)用p(x)的形式来表示出来，则这两个函数必须尽量一致。从图3可以看出，当f(x)与p(x)的高阶导数相等的时候，两条曲线将无限趋近一致。

那么，现在的问题就变成了如何确定图2中p(x)的表达式的系数ai了，同时，又要尽量将这些系数和f(x)的高阶导数联系起来，因此，将图2中p(x)的表达式改写成

图4

因为

图5

再由图4可得:

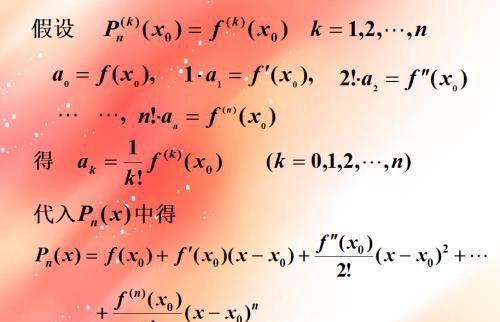
图6

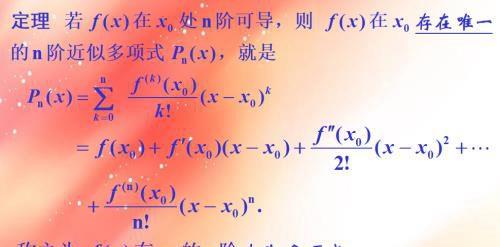
图7

如果包括误差项，则：

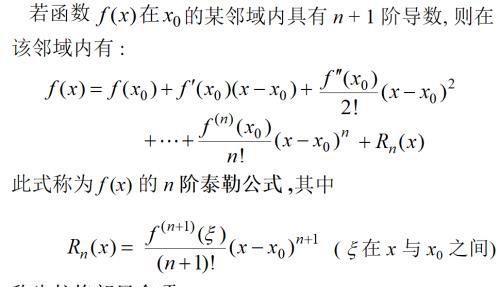
对于麦克劳林级数

常用函数的麦克劳林公式：

以上的证明思路大概是：

1：先确定一个多项式P(x)，再假定要展开的函数 f(x) 和这个多项式各阶导数相等。

2：为了建立多项式系数和函数 f(x) 各阶导数的联系，需要构造一个特别的多项式（图4）。

3：根据这个特别多项式得出系数ai和函数 f(x) 在某一点x0各阶导数之间的联系，从而得出泰勒展开式。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小苹创作整理编辑！