二次函数图像动点问题(二次函数动点)

导语：九上数学：二次函数图像，一动点到两定点距离和最小

题目：

这是九年级上册数学配套练习册《人教金学典》上的一道选择题，学生普遍反映较难。

析解：

本题求△PMF周长的最小值，而两个定点之距FM已为定值，故实质上是求PF+PM最小值。由于已知函数图像上的点到定点F的距离与到x轴的距离始终相等，根据线段公理，PF+PM最小值就是点M到x轴的垂线段之长。

第一步，求FM。如下图所示，作直角三角形，利用勾股定理或直角坐标系内两点间距离公式，易知FM=√[（3--2）^2+（√3）^2]=2。

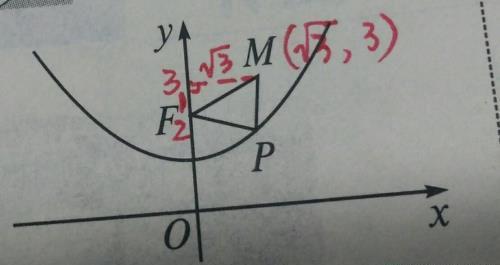
第二步，求PF、PM。如下图所示，过点M作MN⊥x轴，垂足为N，与抛物线交于点P。易知点P横坐标为√3，因其在抛物线上，故点P纵坐标为1/4×（√3）^2+1=7/4=PN=PF。PM=3--7/4。

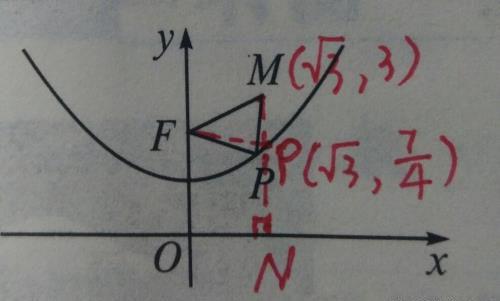
第三步，求△PMF周长。FM+PF+PM=2+7/4+3--7/4=5。故选C项。

反思：

PF+PM最小，一方面利用了线段公理，即两点之间，线段最短。所以本题主要思路就是使PF+PM转化成一条线段。

另一方面，也利用了点到直线的距离，垂线段最短。如下两个草图所示，另取点P两侧各一点P1、P2，分别作到x轴的垂线段P1N1、P2N2，连接MN1、MN2。显然，MP1+P1N1>MN1>MN=PF+PM，MP2十P2N2>MN2>MN=PF+PM。这也算是对该知识点的复习。

提前祝各位条友和学生娃国庆节快乐！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小岑创作整理编辑！