有理数的五大相关概念是什么(有理数及相关概念)
导语:有理数的五大相关概念
知识导航
正数和负数
核心知识点1 正负数的认识 核心知识点2 用正负数表示相反意义的量
核心知识点2 用正负数表示相反意义的量
有理数
核心知识点1 有理数的概念
核心知识点2 有理数的分类

数轴
核心知识点1 数轴的概念及画法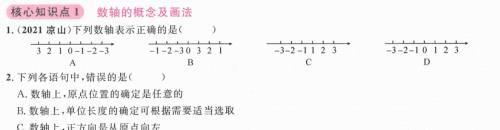 核心知识点2 数轴上的点表示的数
核心知识点2 数轴上的点表示的数
相反数
核心知识点1 相反数的意义 核心知识点2 化简多重符号
核心知识点2 化简多重符号
绝对值
核心知识点1 绝对值的意义及求法 核心知识点2 绝对值性质及应用
核心知识点2 绝对值性质及应用 核心知识点1 运用数轴比较大小
核心知识点1 运用数轴比较大小 核心知识点2 运用法则比较大小
核心知识点2 运用法则比较大小
知识点一、正数与负数
像+3、+1.5、+584等大于0的数,叫做正数; 像-3、-1.5、-584等在正数前面加“-”号的数,叫做负数.
要点诠释:
(1)一个数前面的“+”“-”是这个数的性质符号, “+”常省略,但 “-”不能省略.
(2)用正数和负数表示具有相反意义的量时,哪种为正可任意选择,但习惯把“前进、上升”等规定为正,而把“后退、下降”等规定为负.
(3)0既不是正数也不是负数,它是正数和负数的分界线.
知识点二、有理数的分类
(1)按整数、分数的关系分类: (2)按正数、负数与0的关系分类:
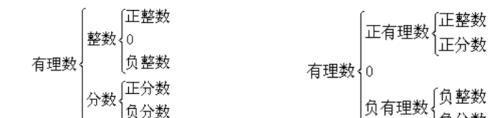
要点诠释:
(1)有理数都可以写成分数的形式,整数也可以看作是分母为1的数.
(2)分数与有限小数、无限循环小数可以互化,所以有限小数和无限循环小数可看作分数,但无限不循环小数不是分数,例如.
(3)正数和零统称为非负数;负数和零统称为非正数;正整数、0、负整数统称整数.
知识点三、数轴
定义:规定了原点、正方向和单位长度的直线叫做数轴.
要点诠释:
(1)定义中的“规定”二字是说原点的选定、正方向的取向、单位长度大小的确定,都是根据需要“规定”的.通常,习惯取向右为正方向.
(2)长度单位与单位长度是不同的,单位长度是根据需要选取的代表“1”的线段,而长度单位是为度量线段的长度而制定的单位.有km、m、dm、cm等.
知识点四、数轴的画法
(1)画一条直线(通常画成水平位置);
(2)在这条直线上取一点作为原点,这点表示0;
(3)规定直线上向右为正方向,画上箭头;
(4)再选取适当的长度,从原点向右每隔一个单位长度取一点,依次标上1,2,3,…从原点向左,每隔一个单位长度取一点,依次标上-1,-2,-3,…
要点诠释:
(1)原点的位置、单位长度的大小可根据实际情况适当选取.
(2)确定单位长度时根据实际情况,有时也可以每隔两个(或更多的)单位长度取一点.
知识点五、数轴与有理数的关系
任何一个有理数都可以用数轴上的点来表示,但数轴上的点不都表示有理数,还可以表示其他数,比如π.
要点诠释:(1)一般地,数轴上原点右边的点表示正数,左边的点表示负数;反过来也对,即正数用数轴上原点右边的点表示,负数用原点左边的点表示,零用原点表示.(2)一般地,在数轴上表示的两个数,右边的数总比左边的数大.
知识点六、相反数
1.定义:如果两个数只有符号不同,那么称其中一个数为另一个数的相反数.特别地,0的相反数是0.
要点诠释:
(1)“只”字是说仅仅是符号不同,其它部分完全相同.(2)“0的相反数是0”是相反数定义的一部分,不能漏掉.
(3)相反数是成对出现的,单独一个数不能说是相反数.
(4)求一个数的相反数,只要在它的前面添上“-”号即可.
2.性质:
(1)互为相反数的两数的点分别位于原点的两旁,且与原点的距离相等(这两个点关于原点对称).
(2)互为相反数的两数和为0.
知识点七、多重符号的化简
多重符号的化简,由数字前面“-”号的个数来确定,若有偶数个时,化简结果为正,如-{-[-(-4)]}=4 ;若有奇数个时,化简结果为负,如-{+[-(-4)]}=-4 .
要点诠释: (1)在一个数的前面添上一个“+”,仍然与原数相同,如+5=5,+(-5)=-5. (2)在一个数的前面添上一个“-”,就成为原数的相反数.如-(-3)就是-3的相反数,因此,-(-3)=3.
知识点八、绝对值
1.定义:在数轴上,一个数所对应的点与原点的距离叫做这个数的绝对值,例如+2的绝对值等于2,记作|+2|=2;-3的绝对值等于3,记作|-3|=3.
要点诠释:
(1)绝对值的代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.即对于任何有理数a都有:
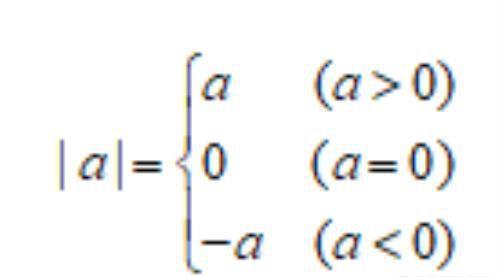
(2)绝对值的几何意义:一个数的绝对值就是表示这个数的点到原点的距离,离原点的距离越远,绝对值越大;离原点的距离越近,绝对值越小.
(3)一个有理数是由符号和绝对值两个方面来确定的.
2.性质:
(1)0除外,绝对值为一正数的数有两个,它们互为相反数.
(2)互为相反数的两个数(0除外)的绝对值相等.
(3)绝对值具有非负性,即任何一个数的绝对值总是正数或0.
知识点九、有理数的大小比较
1.数轴法:在数轴上表示出这两个有理数,左边的数总比右边的数小.
2.法则比较法:
两个数比较大小,按数的性质符号分类,情况如下:
两数同号
同为正号:绝对值大的数大
同为负号:绝对值大的反而小
两数异号
正数大于负数
-数为0
正数与0:正数大于0
负数与0:负数小于0
要点诠释:
利用绝对值比较两个负数的大小的步骤:(1)分别计算两数的绝对值;(2)比较绝对值的大小:
(3)判定两数的大小.
3. 作差法:设a、b为任意数,若a-b>0,则a>b;若a-b=0,则a=b;若a-b<0,a<b;反之成立.
4. 求商法:设a、b为任意正数,若,则;若,则;若,则;反之也成立.若a、b为任意负数,则与上述结论相反.
5. 倒数比较法:如果两个数都大于零,那么倒数大的反而小.

免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小春创作整理编辑!